SuaraJogja.id - Grafik Fungsi Kuadrat, merupakan suatu persamaan dari variable yang memiliki pangkat tertinggi dua.
Fungsi ini berkaitan dengan persamaan kuadrat. Bentuk umum persamaan kuadrat yakni, a2 + bx + c = 0
Dengan f(x) = y yang merupakan variable terikat, x adalah variable bebas, sedangkan a, dan b merupakan koefisien dengan dinamakan persamaan kuadrat, yang mana persamaan kudarat, memiliki variable dengan pangkat tertingginya adalah dua dan berbentuk persamaan.
Bentuk umum dari persamaan kuadrat yakni: dengan x adalah variable bebas, a dan b adalah koefisien, serta c adalah konstanta. Suatu fungsi sangat erat hubungannyan dengan grafik fungsi. Begitu pula fungsi kuadrat, yang memiliki grafik fungsinya sendiri.
Baca Juga:Lerai Siswa Berkelahi di Sekolah, Guru SMA di Dompu Malah Dikeroyok Wali Murid

Untuk diketahui, Grafik fungsi kuadrat berbentuk parabola yang dapat digambarkan menggunakan langkah-langkah tertentu. Untuk lebih jelasnya, simak ulasannya berikut ini.
1. Jenis-Jenis Fungsi Kuadrat
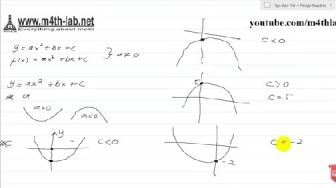
*Jika pada y = ax2+ bx + c nilai b dan c adalah 0, maka fungsi kuadrat menjadi : y = ax2
Yang membuat grafik pada fungsi ini simetris pada x = 0 dan memiliki nilai puncak di titik (0,0)
*Jika pada y = ax2 + bx + c nilai b bernilai 0, maka fungsi kuadrat akan berbentuk : y = ax2 + c
Baca Juga:Sifat-sifat Kubus Lengkap dengan Cara Menghitung Volume Kubus dan Luasnya
Yang membuat grafik pada fungsi ini simetris pada x = 0 dan memiliki titik puncak di (0,c)
*Jika titik puncak ada titik (h,k), maka fungsi kuadrat menjadi : y = a(x – h)2 + k
Dengan hubungan a, b, dan c dengan h,k adalah sebagai berikut :
2.Cara Melukis Grafik Fungsi Kuadrat
Setelah memahami pengertian titik potong dengan sumbu-X dan sumbu-Y, titik puncak atau titik balik parabola serta persamaan sumbu simetri, maka dapat menggambarkan grafik fungsi kuadrat dengan sangat mudah. Langkah-langkah melukis atau menggambar grafik fungsi kuadrat secara umum ada tiga langkah yakni. Pertama, Menemukan titik potong dengan sumbu-X dan sumbu Y.
Kemudian pada langkah kedua, tentukan titik puncak atau titik balik serta persamaan sumbu simetrinya.
Dan langkah ketiga, gambarka koordinat titik-titik hasil langkah 1 dan langkah 2 pada bidang Cartersius. Kemudian hubungan titik-titik tersebut dengan kurva yang mulus dengan memperhatikan apakah parabola tersebut terbuka ke atas atau ke bawah.
3. Keterangan
*Jika D > 0 maka fungsi kuadrat memiliki 2 akar yang berbeda dan memotong di dua titik.
*Jika D = 0 maka fungsi kuadrat memiliki 2 akar yang sama, sehingga kurva hanya akan menyinggung sumbu x di satu titik.
*Jika D < 0 maka kurva tidak menyentuh sumbu x sama sekali.
4. Rumus Grafik Fungsi Kuadrat
Persamaan fungsi kuadrat dapat digambarkan ke dalam koordinat kartesius sehingga diperoleh suatu grafik fungsi kuadrat. Sumbu x disebut sebagai domain dan sumbu y merupakan kodmain. Seringkali bentuk dari grafik fungsi kuadrat adalah parabola. Oleh sebab itu, grafik fungsi ini disebut juga sebagai grafik parabola.
Itulah tadi pengertian tentang grafik fungsi kuadrat mulai dari jenis hingga rumusnya.
Kontributor : Raditya Hermansyah