Sifat Belah Ketupat Beserta Rumus dan Contoh Soalnya

SuaraJogja.id - Sifat belah ketupat. Belah ketupat merupakan salah satu dari bangun datar.

Pengertian dari belah ketupat sendiri adalah salah satu bangun datar dua dimensi yang dibentuk oleh empat buah rusuk sama panjang dan memiliki dua sudut bukan siku-siku, yang masing-masing sudut yang berhadapan memiliki ukuran sama.

Belah ketupat memiliki tiga unsur yang meliputi: sisi, sudut, dan titik sudut. Sisi adalah pembatas daerah belah ketupat, sedangkan sudut adalah bangun yang terbentuk dari pertemuan sisi belah ketupat.

Dan titik sudut adalah titik yang dibentuk dari sudut-sudut belah ketupat.

Baca Juga:Mencari Luas Trapesium: Rumus dan Keterangan Penjelasannya

Melansir dari buku Digital Matematika Bangun Datar karya Rahmat Fajar, dkk., dijelaskan bahwa untuk membedakan bangun belah ketupat dengan bangun datar lain adalah dengan mengetahui ciri-ciri dari belah ketupat.

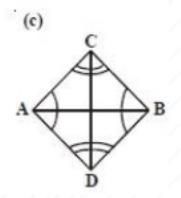
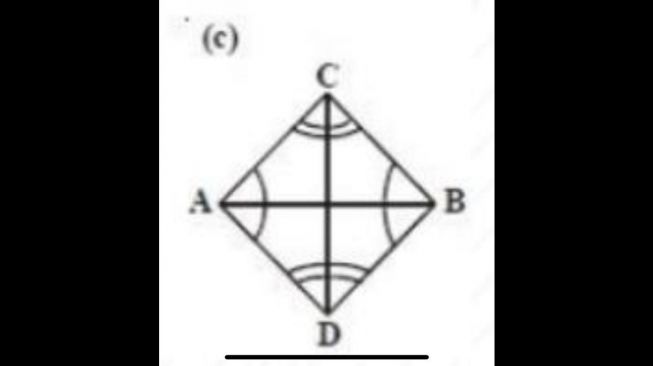
Adapun ciri-ciri atau sifat belah ketupat adalah sebagai berikut:

1. Setiap sudut dibagi dua sama besar oleh diagonal-diagonalnya.
2. Diagonal-diagonalnya berpotongan saling tegak lurus.
3. Sisi-sisinya sama panjang

Dari gambar tersebut bisa diartikan bahwa:

1. Sisi AB = BC = CD = DA (sisi-sisinya sama panjang)
2. Diagonal BD dan AC merupakan sumbu simetri lipat dan membagi bagian menjadi 2 yang sama besar
3. Sudut D = sudut B dan sudut A = sudut C
4. Diagonal BD dan Diagonal AC berpotongan tegak lurus

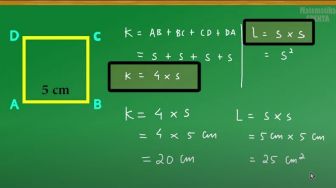
Luas dan keliling belah ketupat
Luas daerah belah ketupat sama dengan setengah hasil kali panjang diagonal-diagonalnya, dengan rumus L = ½ x d1 x d2

Keterangan:

Baca Juga:Memahami Sifat dan Rumus Jajar Genjang

• L = luas
• d1 = Diagonal 1
• d2 = Diagonal 2

sedangkan keliling belah ketupat sama dengan empat kali panjang sisinya, dengan rumus: k = 4 x s

keterangan:

• k = keliling
• s = sisi

Contoh Soal
ABCD adalah belahketupat dengan diagonal AC = 10 satuan panjang, BD = 12 satuan panjang, dan AB = 9 satuan panjang. Maka luas dan keliling dari belah ketupat ABCD adalah:

Jawaban:

Menghitung luas:

L = ½ x AC x BD
L = ½ x 10 x 12
L = 60

Jadi luas daerah belah ketupat ABCD adalah 60 satuan 1 luas.

Menghitung keliling:

K = 4 x AB
K = 4 x 9
K = 36

Jadi keliling daerah belah ketupat ABCD adalah 36 satuan 1 luas.

Demikianlah sifat belah ketupat beserta rumus dan contoh soalnya.

Kontributor : Agung Kurniawan